2019暑期集训第十二讲：高级数据结构（三）

分块

分块是一种思想，对于一些题目，首先线段树等数据结构，分块作为一个备用方案

它擅长做的一些事情

• 区间和
  • 将序列分段，每段长度$T$，那么一共右$n\over T$段，大段维护小段暴力，复杂度$O({n\over T}+T)$
  • 也可以维护很多种前缀和进而做到$O(1)$查询
• 对询问分块
  • 如果操作次数比较少，可以先把操作记下来，在询问的时候加上这些操作的影响
  • T个操作，则修改$O(1)$，询问$O(T)$

莫队

莫队算法是由莫涛提出的算法，可以解决一类离线区间询问问题，适用性极为广泛。同时将其加以扩展，便能轻松处理树上路径询问以及支持修改操作。

形式

假设 n=m，那么对于序列上的区间询问问题，如果从$[l,r]$的答案能够$O(1)$扩展到 $[l-1,r],[l+1,r],[l,r+1],[l,r-1]$（即与 $[l,r]$ 相邻的区间）的答案，那么可以在$O(n\sqrt n)$ 的复杂度内求出所有询问的答案。

实现

• 排序：对于区间$[l,r]$，以$l$所在块的编号为第一关键字，以$r$为第二关键字从小到大排序
• 实现：先排序，顺序处理每一个询问，暴力从上一个区间的答案转移到下一个区间的答案

inline void move(int pos, int sign) {
  // update nowAns
}
void solve() {
  BLOCK_SIZE = int(ceil(pow(n, 0.5)));
  sort(querys, querys + m);
  for (int i = 0; i < m; ++i) {
    const query &q = querys[i];
    while (l > q.l) move(--l, 1);
    while (r < q.r) move(r++, 1);
    while (l < q.l) move(l++, -1);
    while (r > q.r) move(--r, -1);
    ans[q.id] = nowAns;
  }
}

复杂度分析

1. 当n和m同级时，对于每个块内，右端点单调递增，左端点都在块内，所以处理每个块内的询问操作右端点最多移动$n$次，所以所有的询问右端点最多移动$n\cdot {n\over T}$次。而对于所有询问的左端点，每次移动最多$T$次，所以复杂度$O(n\cdot T)$，所以总复杂度$O(n\cdot{n\over T}+n\cdot T)$ 当$T=\sqrt n$时最优达到$O(n\sqrt T)$
2. 当n和m不同级时，对于每个块，右端点最多修改$n$次，每个询问左端点最多移动$T$次，所以复杂度$O({n\over T}\cdot n + mT)$ 当$T={n\over{\sqrt m}}$时最优

例题 小Z的袜子 (HYSBZ-2038)

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命…… 具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。 你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

思路：模板题

某个区间$[l,r]$的答案：

$${\sum_{i是区间内出现的颜色} sum[i]\cdot (sum[i]-1)/2}\over {C_{r-l+1}^2}$$

1. 对询问排序
   1. $[l,r]$，以$l$所在块的编号为第一关键字，r为第二关键字从小到大排序。
2. 暴力维护答案的分子部分即可
3. 可以发现答案分子分母同时将2约掉，分子展开后变成$sum[i]\cdot sum[i] - sum[i]$可以发现对于所有的 i ，$sum[i]$的和将变成$r-l+1$，所以我们只需要维护所有$sum[i]$的平方和即可

#include <iostream>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 50010;
typedef long long ll;
int a[N],be[N],n,m;
ll res = 0,sum[N];
struct node{
    int l,r,id;
    ll A,B;
}q[N];
//如果在同一块，则按照右端点排序，否则按照左端点
bool cmp1(node a,node b){
    return be[a.l] == be[b.l] ? a.r < b.r : a.l < b.l;
}
bool cmp(node a,node b){
    return a.id < b.id;
}
ll gcd(ll a,ll b){return b == 0 ? a : gcd(b,a%b);}
ll S(ll x){return x * x;}
//先减去上一次的影响，修改后再重新加新的影响
void move(int pos,int add){res -= S(sum[a[pos]]);sum[a[pos]] += add;res += S(sum[a[pos]]);}
int main(){
    scanf("%d%d",&n,&m);
    int base = sqrt(n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);q[i].id = i;
        be[i] = (i-1) / base + 1;//be[i]即i在第几块
    }
    for(int i=1;i<=m;i++)scanf("%d%d",&q[i].l,&q[i].r);
    sort(q+1,q+1+m,cmp1);
    int l = 1,r = 0;
    res = 0;//res为当点询问区间内出现的所有颜色的个数平方和
    for(int i=1;i<=m;i++){
        //暴力调整区间，维护res
        while(l < q[i].l)move(l++,-1);
        while(l > q[i].l)move(--l,1);
        while(r < q[i].r)move(++r,1);
        while(r > q[i].r)move(r--,-1);
        if(l == r){
            q[i].A = 0;q[i].B = 1;continue;
        }
        q[i].A  = res - (r - l + 1);//计算答案分子部分
        q[i].B = 1ll * (r - l + 1) * (r - l);//分母部分
        ll g = gcd(q[i].A,q[i].B);//约分
        q[i].A /= g;
        q[i].B /= g;
    }
    sort(q+1,q+1+m,cmp);
    for(int i=1;i<=m;i++){
        printf("%lld/%lld\n",q[i].A,q[i].B);
    }
    return 0;
}

普通莫队优化

可以发现当第一块内的询问处理完之后，r的位置应该特别靠后，但是当移动到下一个块之后，r可能会往前移动很多，比如如下询问

//第一个块
1 50
2 100
//第二个块
12 13
14 100

在完成[2,100]的询问后，r从100-> 13 然后又从13 -> 100。这样显然不如100->100, 100 -> 13。

如何优化？

相邻两块之间r的排序规则相反即可

即奇数块按照升序，偶数快按照降序

Result	Memory	Time
Accepted	3456 kb	1840 ms
Accepted	3456 kb	1392 ms

下面的是优化过的。

bool cmp1(node a,node b){
    return be[a.l] == be[b.l] ? 
        (be[a.l]&1 ? a.r < b.r : a.r > b.r)
        : a.l < b.l;
}

带修改的莫队

考虑普通莫队加入修改修做，如果修改操作可以$O(1)$的应用以及撤销(同时也要维护当前区间的答案)，那么可以在$O(n^{5\over 3})$的复杂度内求出所有询问的答案。

实现: 离线后排序，顺序遍历询问，先将时间转移到当前询问的时间，然后再像普通莫队一样转移区间。

排序方法: 设定块的长度为$S_1,S_2$，按照($\lfloor{l\over S_1}\rfloor \lfloor{r\over S_2}\rfloor,t$)的三元组小到大排序，其中 $t$ 表示这个询问的时刻之前经历过了几次修改操作

复杂度分析：考虑询问序列中的每个小块，小块内每个询问的一二关键字相同。在这个小块内，时间 $t$ 最多变化 $m$ ，对于每个询问，$l,r$ 最多变化 $S_1,S_2$, 一共右$n^2\over {S_1,S_2}$ 个这样的块，相邻块之间转移复杂度是$O(n)$, 总复杂度就是

$O(mS_1+mS_2+{n^2m\over S_1S_2}+{n^3\over S_1S_2})$

当$n,m$同阶时，取$S_1 = S_2 = n^{2\over 3}$ 时可达到最优复杂度$O(n^{5\over 3})$

int l = 0, r = 0, t = 0, nowAns = 0;

inline void move(int pos, int sign) {
    // update nowAns
}

inline void moveTime(int t, int sign) {
    // apply or revoke modification
    // update nowAns
}

void solve() {
    BLOCK_SIZE = int(ceil(pow(n, 2.0 / 3)));
    sort(querys, querys + m);
    for (int i = 0; i < q1; ++i) {
        const query q = querys[i];
        while (t < q.t) moveTime(t++, 1);
        while (t > q.t) moveTime(--t, -1);
        while (l < q.l) move(l++, -1);
        while (l > q.l) move(--l, 1);
        while (r < q.r) move(r++, 1);
        while (r > q.r) move(--r, -1);
        ans[q.id] = nowAns;
    }
}

树分块

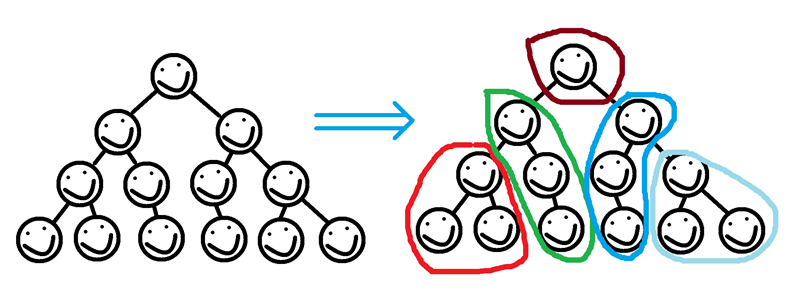
递归处理子树，把当前结点当作栈底，然后递归，回溯回来之后如果栈中结点数量到达某一个标准时，弹出栈中所有的元素分到一个块中，最后递归结束了如果栈中还有元素，那么剩下的这些元素放在新的块中

题目：BZOJ-1086

当块中元素大于B时，立即释放放入到一个新块中，省会可以直接用当前递归到的点，因为它的子节点一定是在栈中的。最后栈中剩下的部分是小于B的，所以可以直接加到上一个块中。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010;
vector<int> G[N];  
int n,B,st[N],sz = 0;
int block_cnt = 0,province[N],be[N];
void dfs(int u,int fa = -1){
    int bottom = sz;//把当前结点当作栈底
    for(int i = 0;i < G[u].size();i++){
        int y = G[u][i];
        if(y == fa)continue;
        dfs(y,u);
        if(sz - bottom >= B){//如果栈中元素大于B
            block_cnt++;//块数++
            while(sz != bottom){
                be[st[sz--]] = block_cnt;
            }
            province[block_cnt] = u;
        }
    }
    st[++sz] = u;//栈中加入该元素
}
int main(){
    scanf("%d%d",&n,&B);
    for(int i=1;i<n;i++){
        int x,y;scanf("%d%d",&x,&y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs(1);
    while(sz)be[st[sz--]] = block_cnt;
    printf("%d\n",block_cnt);
    for(int i=1;i<=n;i++){
        printf("%d ",be[i]);
    }
    puts("");
    for(int i=1;i<=block_cnt;i++){
        printf("%d ",province[i]);
    }
    puts("");
    return 0;
}

树上莫队

参考博客

对于树上的路径询问问题

• O(1)的时间加入或删除一个点的贡献 -> $O(n\sqrt n)$的复杂度求出所有询问的答案

对树上的结点进行分块，离线询问后排序，顺序遍历暴力转移路径（转移时加入或删除路径上的点的贡献即可）。

关于转移路径：首先定义路径：设$T_u$为$u$ 到根的路径上边的集合，那么$u$到$v$ 的路径上的边的集合就是$T_u \triangle T_v$ ($\triangle$ 是对称差）。要从$u\rightarrow v$ 转移到 $u’\rightarrow v’$ 等价于

$$T_u \triangle T_v\rightarrow T_{u'}\triangle T_{v'}$$

根据对称差的性质$Tu\triangle T_u\triangle T{u’} = T_{u’}$ 所以只需要：

$$T_u \triangle T_v \triangle (T_u\triangle T_{u'})\triangle (T_v\triangle T_{v'}) = T_{u'}\triangle T_{v'}$$

体现在程序上就是从$u\rightarrow v$ 转移到$u’ \rightarrow v’$时，暴力遍历路径$u\rightarrow u’$和路径$v\rightarrow v’$上的边，如果一条边已经加入，那么删除它，如果没有加入，就加入它。这样就完成了对称差运算。

复杂度分析：设树分块大小为S，每次转移$u\rightarrow u’$在块内的转移路径长度是$O(S)$的，而$v\rightarrow v’$的转移可以按照$dfs$序来递增，这样复杂度就是$O(ms+{n^2\over S})$

当$S=\sqrt n$时最优

例题 题目传送门

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 40010;
const int M = 100010;
vector<int> G[N],alls;
int be[N],f[N][19],n,m,ans[M],dep[N],u=1,v=1,sum[N],vis[N],a[N],base,cnt;
int res;
int st[N],top;
struct Query{
    int l,r;
    int id;
}q[M];
void dfs(int x,int fa = -1){
    for(int i=1;i<18;i++)
        f[x][i] = f[f[x][i-1]][i-1];
    int bottom = top;
    for(int i = 0;i<G[x].size();i++){
        int y = G[x][i];
        if(y == fa)continue;
        dep[y] = dep[x] + 1;
        f[y][0] = x;
        dfs(y,x);
        if(top - bottom >= base){
            cnt++;
            while(top != bottom){
                be[st[top--]] = cnt;
            }
        }
    }
    st[++top] = x;
}
bool cmp(Query a,Query b){
    return be[a.l] == be[b.l] ? be[a.r] < be[b.r] : be[a.l] < be[b.l];
}
int LCA(int x,int y){
    if(dep[x] > dep[y])swap(x,y);
    for(int i=18;i>=0;i--)if(dep[x] <= dep[f[y][i]]) y = f[y][i];
    if(x == y)return x;
    for(int i=18;i>=0;i--)if(f[x][i] != f[y][i])x = f[x][i],y = f[y][i];
    return f[x][0];
}
void Run(int u){
    if(vis[u] == 1){
        vis[u] = 0;
        if(--sum[a[u]] == 0)res--;
    }
    else{
        vis[u] = 1;
        if(sum[a[u]]++ == 0)res++;
    }
}
void move(int x,int y){
    if(dep[x] < dep[y])swap(x,y);
    while(dep[x] > dep[y])Run(x),x = f[x][0];
    while(x != y)Run(x),Run(y),x = f[x][0],y = f[y][0];
}
int main(){
    scanf("%d%d",&n,&m);
    base = sqrt(n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        alls.push_back(a[i]);
    }
    /*离散化*/
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
    for(int i=1;i<=n;i++){
        int id = lower_bound(alls.begin(),alls.end(),a[i]) - alls.begin() + 1;
        a[i] = id;
    }
    //存树
    for(int i=1;i<n;i++){
        int x,y;scanf("%d%d",&x,&y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dep[1] = 1;//这里如果不单独设为wa
    dfs(1);
    while(top)be[st[top--]] = cnt;
    //存询问
    for(int i=1;i<=m;i++){
        scanf("%d%d",&q[i].l,&q[i].r);
        q[i].id = i;
    }
    sort(q+1,q+1+m,cmp);
    for(int i=1;i<=m;i++){
        if(u != q[i].l){move(u,q[i].l);u=q[i].l;}
        if(v != q[i].r){move(v,q[i].r);v=q[i].r;}
        int anc = LCA(u,v);
        Run(anc);//单独考虑LCA
        ans[q[i].id] = res;
        Run(anc);//
    }
    for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
    return 0;
}

树上带修改的莫队与上面带修改的莫队处理方式相近

块状数组

同进阶指南分块部分

把一个数组分成若干段，$L[i],R[i]$ 分别表示第 $i$ 段的左右端点，$be[i]$ 表示 $i$ 属于第几段。大段维护局部朴素

直接上题

Luogu2801

长度为$n(n\le 1000000)$的数组，$q(q\le 3000)$ 次操作。修改操作即将某个区间的值增加某个不大于1000的值，查询操作即查询某个区间比C大于等于的数有多少个

我们用一个数组$add[i]$来表示第$i$段增量，如果查询区间完全包含第$i$段，那么就相当于是在原数组中查找大于等于$C-add[i]$的数，怎么找？排序后二分找。而对于左右不完整的那部分，直接暴力查询就可以。

对于修改操作。整段的直接增加增量，不完整的直接修改原数组，然后重新排序即可。

假设一段长度为$t$ 则复杂度$O(C(t+{nlog(t)\over t}))$

#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int a[N],b[N],be[N],L[N],R[N],add[N];
char op[3];
int l,r,x;
int n,m;
void change(int l,int r,int x){
    int p = be[l],q = be[r];
    if(p == q){
        for(int i=l;i<=r;i++)a[i] += x;
        for(int i=L[p];i<=R[p];i++)b[i] = a[i];
        sort(b+L[p],b+R[p]+1);
    }
    else{
        for(int i=p+1;i<=q-1;i++)add[i] += x;
        for(int i=l;i<=R[p];i++)a[i] += x;
        for(int i=L[p];i<=R[p];i++)b[i] = a[i];
        sort(b+L[p],b+R[p]+1);
        for(int i=L[q];i<=r;i++)a[i] += x;
        for(int i=L[q];i<=R[q];i++)b[i] = a[i];
        sort(b+L[q],b+R[q]+1);
    }
}
void solve(int l,int r,int x){
    int res = 0;
    int p = be[l],q = be[r];
    if(p == q){
        for(int i=l;i<=r;i++){
            if(a[i] + add[p] >= x)res++;
        }
        printf("%d\n",res);return;
    }
    else{
        for(int i=p+1;i<=q-1;i++){
            res += (R[i]-L[i]+1) - (lower_bound(b+L[i],b+R[i]+1,x-add[i]) - (b+L[i]));
        }
        for(int i=l;i<=R[p];i++)if(a[i] + add[p] >= x)res++;
        for(int i=L[q];i<=r;i++)if(a[i] + add[q] >= x)res++;
        printf("%d\n",res);return ;
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),b[i] = a[i];
    int t = sqrt(n);
    for(int i=1;i<=t;i++){
        L[i] = (i - 1) * t + 1;
        R[i] = i * t;
    }
    if(R[t] < n)t++,L[t] = R[t-1] + 1,R[t] = n;
    for(int i=1;i<=t;i++)for(int j=L[i];j<=R[i];j++)be[j] = i;
    for(int i=1;i<=t;i++){
        sort(b+L[i],b+R[i]+1);
    }
    while(m--){
        scanf("%s%d%d%d",op,&l,&r,&x);
        if(op[0] == 'M')change(l,r,x);
        else solve(l,r,x);
    }
    return 0;
}

关于蓝书上的例题，细节上的问题可以看喔之前写的总结：

蒲公英

磁力块