动态规划(线性,区间,树形)
对于动态规划 我们所需要确定的肯定就是以下几种元素
- 状态(阶段)
我们确定的状态要保证当前的状态不会对于后面的状态产生影响 这个条件也被叫做无后效性 并且这个状态能够表示出所有的状态
2.决策
我们利用什么样的决策从前面一个阶段转移到我当前的阶段过来(可能是前面的阶段去最小值,最大值之类的)
开始写代码的时候要确定状态的起始条件(也就是边界条件) 再确定状态的最总目标 (也就是我们要求的答案)
1.线性dp
具有线性“阶段”划分的动态规划算法被称为线性dp
题目 1:
给定一个包含整数的二维矩阵,子矩形是位于整个阵列内的任何大小为1 * 1或更大的连续子阵列。矩形的总和是该矩形中所有元素的总和。在这个问题中,具有最大和的子矩形被称为最大子矩形。例如,下列数组:
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
其最大子矩形为:
9 2
-4 1
-1 8
它拥有最大和15
对于这个问题 我们当然可以直接暴力枚举这个区间的起始端点和结束端点来求答案,但是这个方案的复杂度太高了,我们可以想到之前做过的最大的连续子序列和的线性dp来解这道题目 这道题目只不过是扩大到了二维而已;
解题思路:我们假设把每一行和看做一个新的元素 然后就是二维的降到了一维的 然后在跑一次一维的连续子序列dp 更新一下答案就好了
具体代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include<bits/stdc++.h>
using namespace std;
int a[102][102],sum[102][102],dp[102];
int main()
{
int n;
cin>>n;
memset(sum,0,sizeof(sum));
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
cin>>a[i][j];
sum[i][j] = sum[i][j-1] + a[i][j];
}
}
int ans = -1000;
for(int j = 1; j <= n ; j++)
{
for(int k = 0; k < j; k++)
{
for(int p = 0; p < 102 ; p++) dp[p] = -1000;
dp[0] = 0;
for(int i = 1; i <= n; i++)
{
dp[i] = max(sum[i][j] - sum[i][k],dp[i-1] + sum[i][j] - sum[i][k]);
ans = max(ans,dp[i]);
}
}
}
cout<<ans<<endl;
return 0;
}
|
题目2:
就是给你一个序列 让你求这个序列的最长下降子序列 并且就子序列的方案数 这个方案数对于相同的价格序列需要去重(也就是不能多算)
这个题目的前半部分求最长下降子序列我们应该都是会求的 但是后面的计数我们要怎么考虑呢
计数的话就是从后面开始个g[i] 表示以当前第i位为结尾的最长下降子序列的长度的个数 当满足
dp[i] = dp[j] + 1 并且 a[j] > a[i] 那么就说明g[i] 可以由 g[j] 转移过来 g[i] += g[j]; 现在考虑怎么去重
假设我现在有如右一个下降子序列 5 4 3 …. 2 1 那么如果在 3 的后面还有一个3的话 是不是后面的3能够构成的下降子序列我前面的这个3其实也是能够构成的 那么我们去重的话就可以从这里入手 我们设值一个g数组,g[i]表示以i为结尾的最长下降子序列有多少个 这时候从i往前面扫过去 如果前面的a[j] == a[i] 的话 就把g[j]置为0 这样就不会出现重复的情况了 简单的来说就是把a[j] 的方案数嫁接到了 a[i] 上面了 因为序列等效了 就没有必要有g[j]了
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 5e3 + 10;
int a[maxn],dp[maxn],g[maxn];
int main()
{
int n;
scanf("%d",&n);
for(int i = 0 ; i < n; i++)
{
scanf("%d",&a[i]);
}
int ans = 0;
for(int i = 0; i < n; i++)
{
dp[i] = 1;
for(int j = 0; j < i; j++)
{
if(a[i] < a[j]) dp[i] = max(dp[i],dp[j] + 1);
}
if(dp[i] == 1) g[i] = 1;
for(int j = 0; j < i; j++)
{
if(a[j] == a[i]) g[j] = 0;
}
for(int j = 0; j < i; j++)
{
if(a[i] < a[j] && dp[i] == dp[j] + 1) g[i] += g[j];
}
ans = max(ans,dp[i]);
}
printf("%d ",ans);
int cnt = 0;
for(int i = 0; i < n; i++)
{
if(dp[i] == ans) cnt += g[i];
}
printf("%d",cnt);
return 0;
}
|
题目3:给你一堆箱子的长宽高 问你对多能够利用这些箱子叠的多高 注意就是底面一直要是能够完全覆盖的
思路 :一个箱子可以有六种形态 假设初始给的 x y z 那么我们可以有 x为长 y宽的长方形为底 z为高 的立方体 也可以有以x为长 y为宽的长方形 z为高的长方体 所以共有6种 预先按照 底面的长方形 的长与宽先排序 (如果不排序取的不是最优的) 设dp[i] 表示第i个能够构成的最长高 边界条件 dp[1] = rec[i].h 最值目标 max(dp[i]) ;转移方程: dp[i] = max(dp[i],dp[j]+rec[i].h);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 200;
int dp[maxn];
int m = 0;
struct node{
int x;
int y;
int h;
}rec[maxn];
void add(int a,int b,int c)
{
rec[m].x = a,rec[m].y = b,rec[m].h = c,m++;
rec[m].x = a,rec[m].y = c,rec[m].h = b,m++;
rec[m].x = b,rec[m].y = a,rec[m].h = c,m++;
rec[m].x = b,rec[m].y = c,rec[m].h = a,m++;
rec[m].x = c,rec[m].y = b,rec[m].h = a,m++;
rec[m].x = c,rec[m].y = a,rec[m].h = b,m++;
}
bool cmp(node a,node b)
{
if(a.x!=b.x)
return a.x>b.x;
return a.y>b.y;
}
int main()
{
int n,t = 1;
while(cin>>n)
{
m = 0;
if(!n)
break;
int a,b,c,ans = 0;
for(int i = 0; i < n; i++)
{
cin>>a>>b>>c;
add(a,b,c);
}
sort(rec,rec+m,cmp);
for(int i = 0; i < m; i++)
{
dp[i] = rec[i].h;
for(int j = 0; j <= i; j++)
{
if(rec[j].x>rec[i].x&&rec[j].y>rec[i].y)
dp[i] = max(dp[i],dp[j]+rec[i].h);
ans = max(ans,dp[i]);
}
}
cout<<"Case "<<t<<": maximum height = "<<ans<<endl;
t++;
}
}
|
题目 4: 求最长上升公共子序列 并且要求记录所有的路径
前一问的话我们之前其实是都学过的 这题的难点就是在于后面的求出所有的公共路径的,求公共路径我们需要用到两个辅助数组,这两个数组的作用是一样的,只是作用的串不一样 , posa [i] [j] 表示第i位之前字符j第一次出现的位置 具体看代码
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| #include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;
const int maxn = 100;
int dp[maxn][maxn],posa[maxn][30],posb[maxn][30],tot = 0,t_len;
char a[maxn],b[maxn];
string ans[1000];
void dfs(string s,int x,int y,int len)
{
if(s.size() == t_len)
{
reverse(s.begin(),s.end());
ans[tot++] = s;return ;
}
if(x < 1 || y < 1) return ;
if(a[x] == b[y])
{
dfs(s + a[x], x - 1,y - 1,len - 1);
}
else
{
for(int i = 0; i < 26; i++)
{
if(dp[posa[x][i]][posb[y][i]] == len)
{
dfs(s,posa[x][i],posb[y][i],len);
}
}
}
}
int main()
{
string x,y;
cin>>x>>y;
for(int i = 0; i < x.size(); i++) a[i + 1] = x[i];
for(int j = 0; j < y.size(); j++) b[j + 1] = y[j];
int n = x.size(),m = y.size();
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(a[i] == b[j])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else dp[i][j] = max(dp[i - 1][j],dp[i][j - 1]);
}
}
t_len = dp[n][m];
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < 26; j++)
{
if(a[i] == 'a' + j) posa[i][j] = i;
else posa[i][j] = posa[i - 1][j];
}
}
for(int i = 1; i <= m; i++)
{
for(int j = 0; j < 26; j++)
{
if(b[i] == 'a' + j) posb[i][j] = i;
else posb[i][j] = posb[i-1][j];
}
}
string s = "";
dfs(s,n,m,t_len);
sort(ans,ans + tot);
for(int i = 0; i < tot; i++)
{
cout<<ans[i]<<endl;
}
return 0;
}
|
区间dp
区间DP过程大致相同,大都满足第一层循环枚举长度,第二层循环枚举起点。最内层往往有两种形式,第一种是需要在[i,j]中找一个分割点k使得将[i,j]分成[i,k]和[k+1,j]这样两个区间能够得到最优解
第二种形式是[i,j]可以由[i,j-1]或者[i,j+1]转移过来.重要的是找出新添加的元素(可以是k或者i)与之前那个len-1长度区间的关系
题目5:多边形游戏”是一款单人益智游戏。
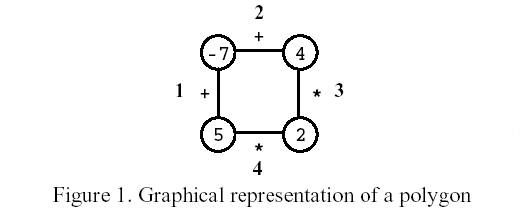
游戏开始时,给定玩家一个具有N个顶点N条边(编号1-N)的多边形,如图1所示,其中N = 4。
每个顶点上写有一个整数,每个边上标有一个运算符+(加号)或运算符*(乘号)。

第一步,玩家选择一条边,将它删除。
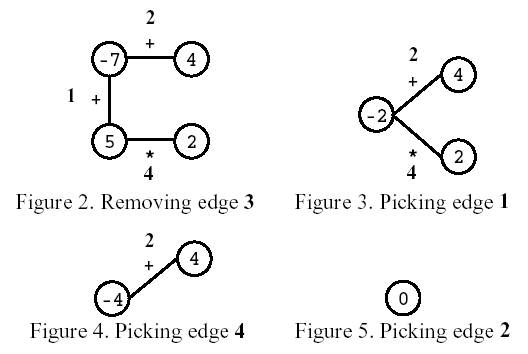
接下来在进行N-1步,在每一步中,玩家选择一条边,把这条边以及该边连接的两个顶点用一个新的顶点代替,新顶点上的整数值等于删去的两个顶点上的数按照删去的边上标有的符号进行计算得到的结果。
下面是用图1给出的四边形进行游戏的全过程。

最终,游戏仅剩一个顶点,顶点上的数值就是玩家的得分,上图玩家得分为0。
请计算对于给定的N边形,玩家最高能获得多少分,以及第一步有哪些策略可以使玩家获得最高得分
思路:区间dp问题,思路的话就是上面讲的区间dp的第一种形式 我们可以设dp[l] [r] 表示区间能够获得的最大值 那么这个区间肯定是由两个子区间通过两个子区间之间的乘号或者加号连接起来的 需要在[i,j]中找一个分割点k使得将[i,j]分成[i,k]和[k+1,j]这样两个区间能够得到最优解dp[l] [j] 不过这个题目因为有乘号和负数的干扰 所以我们还是需要记录区间的最小值和最大值这两个属性 因为区间的最大值可能有两个最大的整数转移过来 也有可能由两个最小的整数相乘转移过来 环形的处理的话就是将其拆乘一个链。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include<bits/stdc++.h>
using namespace std;
const int maxn = 510;
const int MA = 1e9+10;
char a[maxn];
int num[maxn];
int dpmax[maxn][maxn],dpmin[maxn][maxn];
vector<int> ans;
int main()
{
int n;
cin>>n;
memset(dpmax,-128,sizeof(dpmax));
memset(dpmin,0x3f3f,sizeof(dpmin));
for(int i = 0; i < 2*n; i++)
{
if(i%2==0)
{
cin>>a[i];
a[i+2*n] = a[i];
}
else
{
cin>>num[i];
num[i+2*n] = num[i];
dpmin[i][i] = num[i];
dpmax[i][i] = num[i];
dpmin[i+2*n][i+2*n] = num[i];
dpmax[i+2*n][i+2*n] = num[i];
}
}
for(int len = 2; len <= 2*n; len+=2)
{
for(int l = 1; l + len <= 4*n ; l+=2)
{
int r = len + l ;
for(int k = l; k < r; k+=2)
{
if(a[k+1]=='t')
{
dpmax[l][r] = max(dpmax[l][r],dpmax[l][k]+dpmax[k+2][r]);
dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]+dpmin[k+2][r]);
}
else
{
dpmax[l][r] = max(dpmax[l][r],dpmax[l][k]*dpmax[k+2][r]);
dpmax[l][r] = max(dpmax[l][r],dpmin[l][k]*dpmin[k+2][r]);
dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]*dpmin[k+2][r]);
dpmin[l][r] = min(dpmin[l][r],dpmax[l][k]*dpmin[k+2][r]);
dpmin[l][r] = min(dpmin[l][r],dpmin[l][k]*dpmax[k+2][r]);
}
}
}
}
int ret = 0;
for(int i = 1; i <= 2*n; i+=2) ret = max(ret,dpmax[i][2*n+i-2]);
for(int i = 1; i <= 2*n; i+=2) if(dpmax[i][2*n+i-2]==ret) ans.push_back((i+1)/2);
cout<<ret<<endl;
for(int i = 0; i < ans.size(); i++) cout<<ans[i]<<" ";
return 0;
}
|
题目6 : 求一个区间有多少个回文子序列 注意子序列是可以不连续的
思路:
因为是区间dp 那么我们就可以想到用dp[i] [j]来表示区间l到r之间的回文串的个数 边界条件就是l == r 此时dp[l] [r] = 1 对于任意一个区间都有状态转移方程 dp[l] [r] =(dp[l] [r-1] + dp[l+1] [r] - dp[l+1] [r-1] + mod) % mod; 这个式子画一个图 在利用容斥原理就可以的出来 然后就是要特判一下如果s[l] == s[r] 的画 就需要再加上
dp[l] [r] = (dp[l+1] [r-1] + dp[l] [r] + 1 + mod) % mod; 以为上面的式子成立的花 那么就可以多 dp[l+1] [r-1] 个回文串 加1的话是加上 s[l] 与 s[r] 这两个字符组成的回文串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
const int mod = 10007;
int dp[maxn][maxn];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
string s;
cin>>s;
for(int i = 0; i < maxn; i++)
{
for(int j = 0;j < maxn; j++)
{
if(i == j) dp[i][j] = 1;
else dp[i][j] = 0;
}
}
for(int len = 1; len < s.size(); len ++)
{
for(int l = 0; l + len < s.size(); l++)
{
int r = len + l;
dp[l][r] =(dp[l][r-1] + dp[l+1][r] - dp[l+1][r-1] + mod) % mod;
if(s[l] == s[r]) dp[l][r] = (dp[l+1][r-1] + dp[l][r] + 1 + mod) % mod;
}
}
printf("%d\n",dp[0][s.size()-1]);
}
return 0;
}
|
题目7 有n个人排成一排要上台表演,每个人有一个屌丝值pi。第i个上台表演的人,他的不满意度为(i-1)*pi。
现在有一个类似于栈的黑屋子,你可以让某些人进入这个黑屋子。这些人要按照排的顺序来,那么对于排在最前面的人,
就有两个选择:
(1)让他直接上台表演;
(2)让他暂时进黑屋子。
现在请你选择一个合理的调度顺序,使得最后的总不满意度最小?
思路:这个可以划分成一个个子区间来求解 设dp[l] [r] 表示l 到 r直接最小的屌丝值为多少,那么我们肯定关心的就是第一个人到底是排在第几位的 如果他排在第k位的话 那么 2 ~( l + k - 1) 这些人肯定就排在他的前面 就可以再把 2 ~( l + k - 1)这里人在看成一个子区间来求解 (l + k) ~ r 这些人肯定排在前面的k个人后面 我们就得把前面的k个人对于他们的影响给消除掉 也就是在这个基础上加上 k * (sum[r] - sum[l + k - 1]) 那么对于后面的 (l + k) ~ r这个区间就又可以看成一个子区间来求解
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
const int inf = 0x3f3f3f3f;
int dp[maxn][maxn],sum[maxn],a[maxn];
int solve(int l,int r)
{
int ans = dp[l][r];
if(ans != inf) return dp[l][r];
if(l >= r) return 0;
for(int i = l; i <= r; i++)
{
for(int k = 1; k <= r - l + 1;k ++)
{
ans = min(ans,solve(l + 1,l + k - 1) + (k - 1)*a[l] + k * (sum[r] - sum[l + k - 1]) + solve(l + k,r));
}
}
return dp[l][r] = ans;
}
int main()
{
int t,cas = 0;
cin>>t;
while(t--)
{
cas++;
int n;
scanf("%d",&n);
memset(dp,0x3f,sizeof dp);
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
sum[i] = sum[i - 1] + a[i];
}
printf("Case #%d: %d\n", cas, solve(1,n));
}
return 0;
}
|
树形dp
树的特征
1.N个点 只有N-1条边的无向图
2.无向图里 任意两点有且只有一条路
3.一个点只有一个前驱 但可以有多个后继
4.无向图没有环
树形DP
由于树有着天然的递归结构 父子结构 而且它作为一种特殊的图 可以描述许多复杂的信息 因此在树就成了一种很适合DP的框架
问题:给你一棵树 要求用最少的代价(最大的收益)完成给定的操作
树形DP 一般来说都是从叶子从而推出根 当然 从根推叶子的情况也有 不过很少(本蒟蒻还没有做到过~)
一般实现方式: DFS(包括记忆化搜索),递推等
题目8:
就是给你一棵树,每个节点有一个权重,如果你选择了根节点的话 那么他的子节点就不能再次选择,如果你选择子节点的话那么根节点就不能在选
如果是线型的一串一维数组的话 不能选择相邻的数字 要让选择的数的和最大
那么就有递推方程dp[i] = max(dp[i-1],dp[i-2] + a[i])
max里面前一个式子代表我不选a[i] 那么就能从dp[i-1] 转移过来
后面一个代表我选了这个 那么就是从dp[i-2] + a[i] 转移过来
两者取最大值就是我们需要的答案 那么这题的话就可以用这个思想
如果我们选择了这个节点的值的话 我们就只能从这个节点出发的下下一层转移了 下一层不能选了
如果我们不选这个节点 我们直接从下一层节点转移就好了 两者取最大值
代码如下 :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include<bits/stdc++.h>
using namespace std;
const int maxn = 6010;
int val[maxn] , in[maxn];
int dp[maxn] = {0};
vector<int> g[maxn];
int dfs(int root)
{
int tans = dp[root];
if(tans!=0) return tans;
if(g[root].size() == 0) return val[root];
int ans = val[root] , ans1 = 0 ;
for(int i = 0 ; i < g[root].size(); i++)
{
for(int j = 0 ; j < g[g[root][i]].size(); j++)
{
ans += dfs(g[g[root][i]][j]);
}
ans1 += dfs(g[root][i]);
tans = max(ans1,ans);
}
return dp[root] = tans;
}
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++)
{
cin>>val[i];
}
int u,v;
while(cin>>u>>v&&u!=0)
{
g[v].push_back(u);
in[u]++;
}
int root , ans = 0;
for(int i = 1; i <= n; i++)
{
if(in[i]==0) root = i;
}
ans = dfs(root);
cout<<ans<<endl;
}
|
对于树形dp中的换根(二次扫描法) 题目一般会让你算出以每一个节点为根的某些值 然后再在这些值中取最大值或者最小值,这时候你就需要找到每个根节点直接的练习,利用第一次dfs出来的数据,再根据节点之间的关系,进行第二次dfs算出以其他节点为根的时候的最大值
题目9:首先给你一颗树 树的叶子节点就是汇点,就是可以无穷尽的流出水量,每条边有一个权值说明这条边的最大能够流出的水量,现在让你选择一个根节点,也就是源点,源点可以流出无穷多的水量,问你选择那一个节点为源点能够让流出的总水量最大。
思路:dfs+换根 因为这个题目是让你选择一个节点,然后这个根节点的出水量最大,如果你每一个节点每一个节点的去dfs一次的话,时间复杂度肯定是爆炸的,其实我们可以找规律,然后利用一次dfs进行第二次dfs算出来的值推出用其他节点做为源点(也就是根节点)是的最大流水,也就是二次扫描。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn = 4e5+10;
const int inf = 1000000000;
typedef long long ll;
ll t_ans = 0;
ll sz[maxn];
vector< pair<int,ll> > g[maxn];
ll dfs1(int son,int fa)
{
if(g[son].size() == 1) return inf;
ll sum = 0;
for(int i = 0; i < g[son].size(); i++)
{
int u = g[son][i].first;
ll w = g[son][i].second;
if(u==fa) continue;
ll temp = dfs1(u,son);
sum += min(w,temp);
}
sz[son] = sum;
return sum;
}
void dfs2(int son,int fa,ll val)
{
if(g[son].size() == 1) return ;
t_ans = max(t_ans,val);
for(int i = 0; i < g[son].size(); i++)
{
int u = g[son][i].first;
if(u==fa || g[u].size() == 1) continue;
ll w = g[son][i].second;
ll temp = sz[u] + min(w,val - min(w,sz[u]));
dfs2(u,son,temp);
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
t_ans = 0;
scanf("%d",&n);
for(int i = 1; i <= n; i++)
{
g[i].clear();
}
for(int i = 0; i < n - 1; i++)
{
int u,v;
ll w;
scanf("%d%d%lld",&u,&v,&w);
g[u].push_back(make_pair(v,w));
g[v].push_back(make_pair(u,w));
}
ll ans = dfs1(1,-1);
dfs2(1,-1,ans);
printf("%lld\n",t_ans);
}
return 0;
}
|
题目10: 就是问你以每个节点为根的树离叶子节点最长的距离是多少,一次输出每一个节点的距离
思路 :dfs + 换根 也就是二次dfs扫描 不过这个题目需要记录一个最大值和次大值才能完成二次dfs
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
| #include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
int e[maxn],ne[maxn],idx,h[maxn],val[maxn];
int szma[maxn],szmi[maxn],in[maxn],t_ans[maxn];
void add(int a,int b,int w)
{
e[idx] = b,ne[idx] = h[a],val[idx] = w,h[a] = idx++;
}
int dfs1(int now,int fa)
{
szma[now] = 0,szmi[now] = 0;
for(int i = h[now]; i != -1; i = ne[i])
{
int j = e[i],w = val[i];
if(j == fa) continue;
int ne_ma = dfs1(j,now);
if(szma[now] <= w + ne_ma)
{
int temp = szma[now];
szma[now] = w + ne_ma;
szmi[now] = temp;
}
if(w + ne_ma < szma[now] && w + ne_ma >= szmi[now]) szmi[now] = ne_ma + w;
}
return szma[now];
}
void dfs2(int now,int fa,int mid,int mid2)
{
for(int i = h[now]; i != -1; i = ne[i])
{
int j = e[i],w = val[i];
if(j == fa) continue;
int tempmid = mid,tempmid2 = mid2;
if(tempmid != szma[j] + w)
{
if(szma[j] < tempmid + w)
{
tempmid2 = szma[j];
tempmid = tempmid + w;
}
else
{
tempmid2 = max(tempmid + w,szmi[j]);
tempmid = szma[j];
}
t_ans[j] = tempmid;
dfs2(j,now,t_ans[j],tempmid2);
}
else
{
if(szma[j] > tempmid2 + w)
{
tempmid2 = max(szmi[j],tempmid2 + w);
tempmid = szma[j];
t_ans[j] = tempmid;
dfs2(j,now,t_ans[j],tempmid2);
}
else
{
tempmid = tempmid2 + w;
tempmid2 = szma[j];
t_ans[j] = tempmid;
dfs2(j,now,t_ans[j],tempmid2);
}
}
}
}
void init()
{
idx = 0;
for(int i = 0; i <= n; i++) ne[i] = 0;
for(int i = 0; i <= n; i++) h[i] = -1;
for(int i = 0; i <= n; i++) e[i] = 0;
for(int i = 0; i <= n; i++) t_ans[i] = 0;
for(int i = 0; i <= n; i++) val[i] = 0;
for(int i = 0; i <= n; i++) szma[i] = 0;
for(int i = 0; i <= n; i++) szmi[i] = 0;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
init();
for(int i = 2 ; i <= n; i++)
{
int u,w;
scanf("%d%d",&u,&w);
add(i,u,w);
add(u,i,w);
}
int ans = dfs1(1,-1);
t_ans[1] = ans;
dfs2(1,-1,ans,szmi[1]);
for(int i = 1; i <= n; i++)
{
printf("%d\n",t_ans[i]);
}
}
return 0;
}
|
题目11: 给你一颗树 让你任选一个节点为根节点 你要最大化所有子树的顶点数之和 让你输出这个最大值
思路: dfs加换根 到时候具体画图来解释
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include<iostream>
#include<vector>
#include<cstdio>
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
ll sz[maxn],ans = 0,n;
vector<int> g[maxn];
void dfs1(int son,int fa)
{
for(int i = 0; i < g[son].size(); i++)
{
int u = g[son][i];
if(u==fa) continue;
dfs1(u,son);
sz[son] += sz[u];
}
sz[son] += 1;
ans += sz[son];
}
void dfs2(int son,int fa,ll val)
{
for(int i = 0; i < g[son].size(); i++)
{
int u = g[son][i];
if(u==fa) continue;
ll mid = val - sz[u] + n - sz[u];
ans = max(ans,mid);
dfs2(u,son,mid);
}
}
int main()
{
scanf("%d",&n);
for(int i = 0; i < n - 1; i++)
{
int u,v;
scanf("%d%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
dfs1(1,-1);
dfs2(1,-1,ans);
cout<<ans<<endl;
}
|